In nearly every class across the country the Autumn term’s maths learning starts with number: place value, magnitude – ordering and comparing number. A very good place to start if you ask me, as it is arguably the ‘key stone’ to all maths learning. I would say that without a secure understanding of number most other maths learning, especially numeracy, becomes a series of memorised processes using digits rather than numbers.
What do I mean by Numeracy?
I was fortunate to hear Mahesh Sharma speak at the British Dyslexia Association’s Maths and dyscalculia day and in his provided notes he defines numeracy as:
“…the ability to execute standard whole number operations/algorithms correctly, consistently, and fluently with understanding and estimate, calculate accurately and efficiently, both mentally and on paper using a range of calculation strategies and means.” (2019, pg 19)
In summary I think pupils need to be able to:
- identify the value of the numbers in the calculation
- choose the best strategy to solve the calculation
- understand what is happening to the values whilst carrying out the calculation
- complete the calculation accurately
- repeat this process many times
I would argue that some pupils can do the last two bullet points but can’t do the first three. These pupils have learnt a process with digits rather than becoming numerate. I think this is proved over and over by pupils who automatically use standard written methods for any calculation with what seems like very little consideration for the values in the calculations. For example: 245 + 99, £10 - £3.99, 3682 ÷ 1 and 816 x 10 would be answered -
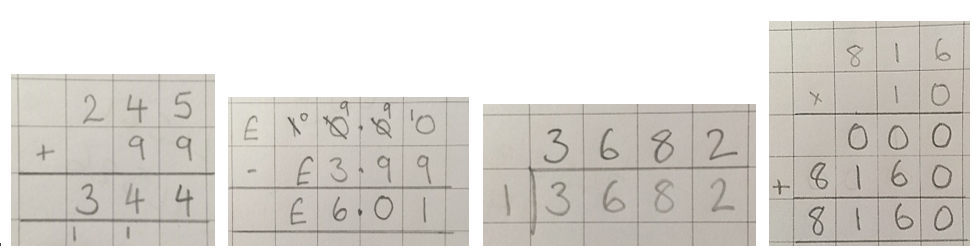
The calculations have been answered accurately and pupils do repeat this many times but pupils have not: identified the value of the numbers in the calculations, chosen the best strategy or applied their understanding of number to help them understand what is happening to the values. They are not secure with number. In these examples the pupils have been accurate but a lack of understanding of number can lead to many errors being caused or misconceptions being repeated over and over again.
In these addition and subtraction examples try and work out what has gone wrong.
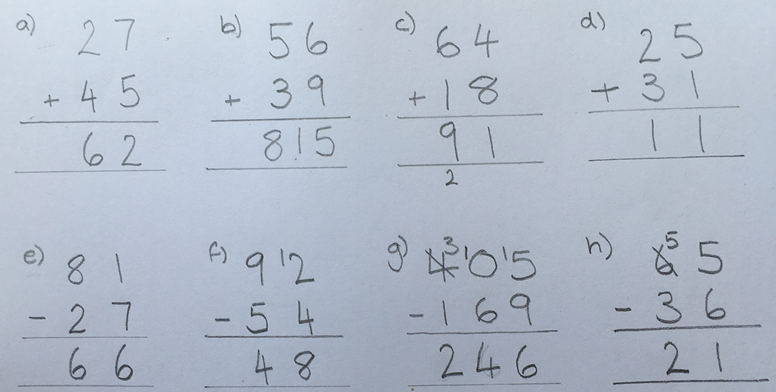
a. not included the additional ten regrouped when adding the ones
b. included all 15 ones in the answer, hasn’t regrouped
c. recognised that there are 12 ones but put the 1 ten in the answer and carried the 2
d. added together the four digits in the calculation 2+5+3+1
e. taken the biggest digit away from the smallest digit in the ones column
f. recognised the need to regroup to be able to take away 4 but not shown that there is now 8 tens in 92
g. recognised the need to regroup but unsure about how to regroup with a no tens
h. recognised that 5 ones is less than 6 ones so shown borrowing a ten but not changes the 5 ones to 15 ones and then taken the biggest digit from the smallest.
In all cases the errors are caused by a lack of understanding of place value.
What does the intervention need to be to help stop these errors?
In my experience what pupils who makes these errors is definitely DO NOT is need more practice of column addition and subtraction. In most cases pupils need to secure their understanding of what happens to tens and ones when counting up and down – regrouping ten ones for a ten when counting up and regrouping ten ones for ten when counting down. Once secure with this they need to be able to regroup numbers into hundreds, tens, ones in a number of ways.
I have found that one of the best ways to support pupils in securing this understanding is to play a simple game sometimes it is called banker, other times it is called race to 50/100/zero.
To play the game the pupils need a place value chart with either hundreds, tens and ones or just tens and ones depending on your start and end points and possibly the age of the pupils. In either case it is important that there are two tens frames embedded in the ones column.
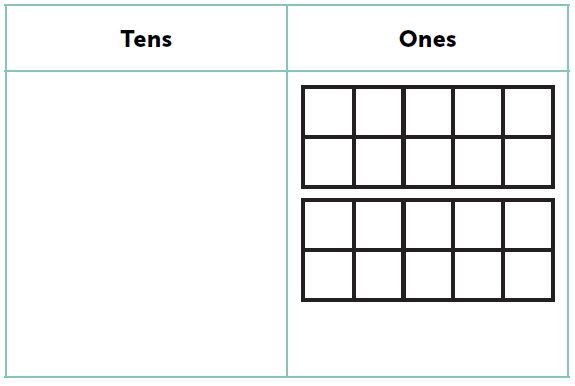
The embedded tens frames enable the pupil to recognise by looking when they have more than ten ones so knows that regrouping needs to happen. The easiest way to generate the number being added each time is by rolling a dice (a ten sided dice works best but an ordinary dotty dice works too). When using the game to count up to a given number the pupil rolls the dice and adds the same number of base-10 ones cubes to the chart as the number rolled. So if 7 is rolled seven cubes are added. At this point encourage the pupil to subitise how many more to ten – the tens frame supports this. Once more than ten ones cubes are in the chart the pupil will need to regroup. The pupil say the total and how it is represented, identify what is going to be regrouped and then restate the total after the regrouping and how it is now represented.
For example:
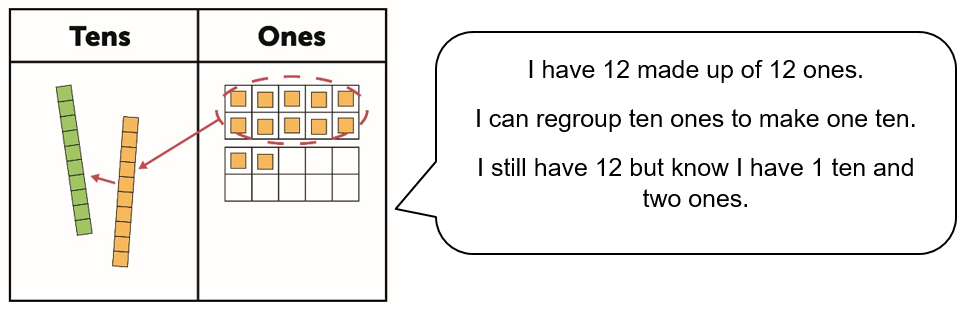
When the pupil groups ten ones for a ten ensure that they understand that this is the same value. The base-10 works really well for this as ten ones cubes is exactly the same size as a tens rod. This regrouping and explanation of what is happening needs to happen every time there is more than ten ones.
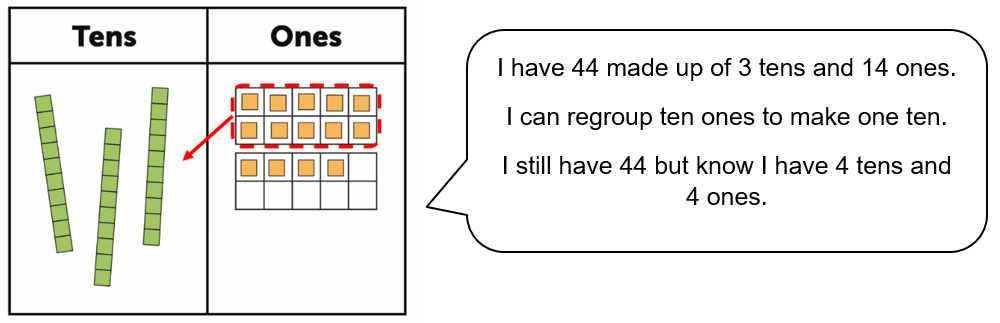
This game needs to be play repeatedly because as well as developing understanding of regrouping they will also be developing their visualisation of the number and conservation of number recognising that as regrouping is done the total amount doesn’t change.
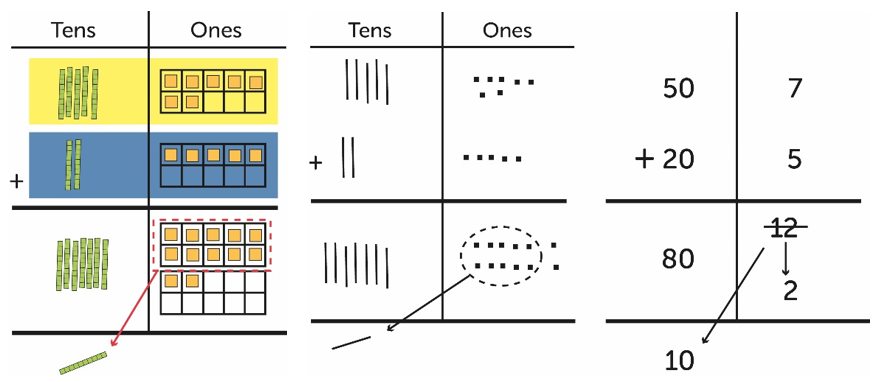
If you think back to the errors made in the addition calculations (a-d) all of those errors were caused by a lack of understanding of regrouping the ones (a-c) or not understanding the value of the digits (d). To bridge the gap between the improved understanding of regrouping from the game to the written strategy expanded column addition will help to make the place value explicit, initially the calculation can be done using the base-10, then represented pictorially and finally written.
For example for 57 + 25:
To support the understanding of how regrouping is needed in subtraction again an adaptation of the ‘Banker’, ‘Race to…’ games are the best starting point. The same place value chart is used but this time the pupils start with an amount and need to count down. This time when a decade boundary is crossed a ten will need to be regrouped for ten ones when there isn’t enough ones to take away. As before the explanation of the regrouping needs to be articulated each time it takes place.
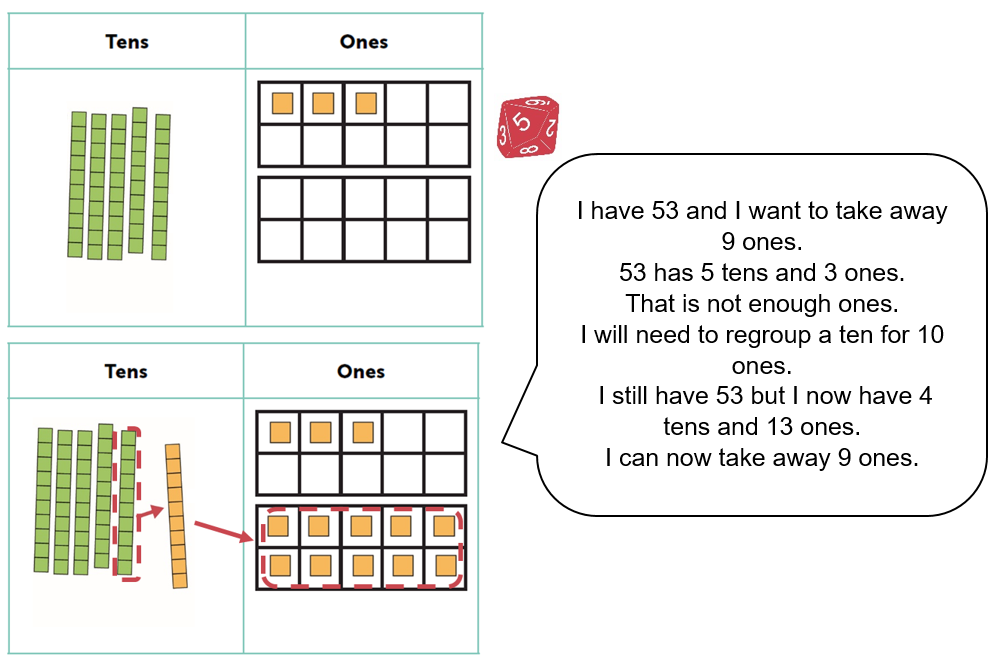
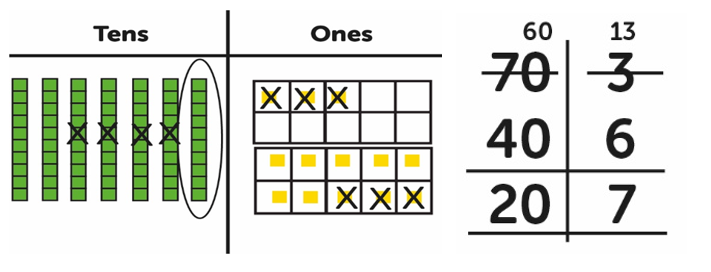
As with addition all the errors made with in the subtraction calculations above were caused by insecure place value understanding. The most common mistake I see with subtraction is like in calculation e) when pupils take the smaller digit from the biggest, practice of regrouping using the ‘banker’ game will help reduce this common mistake. Then using the CPA (concrete, pictorial and abstract) approach and an expanded written method the link between the regrouping when counting back and written subtraction can be made.
For example 73 - 46:
It is the practical element of the game using explicit place value equipment (base-10) physically regrouping the tens and ones alongside the verbal explanation of what is being done that helps to secure the understanding of what is happening to the numbers as they pass through decades. When this is then linked to a calculation strategy pupils make the connections and are able to carry out the process of column addition or subtraction with a much better understanding both of the process and the value of the numbers within them.
They have become more numerate.
Thinking back to Sharma’s definition of numeracy what this blog hasn’t covered is whether column addition is the best strategy or whether another strategy would be better. Considering the original examples:
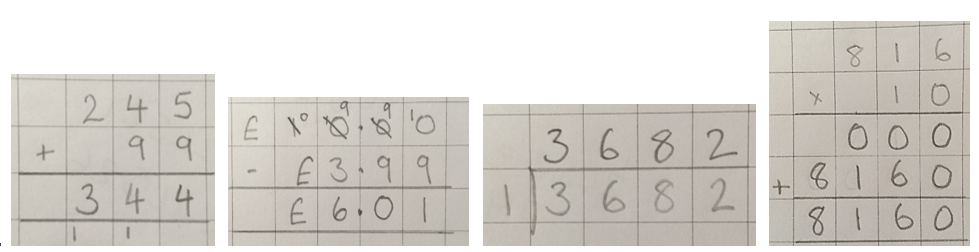
Arguably all of these would all be better answered using a mental strategy but that’s another blog.
To find out more please book onto the following course
Mathematics intervention using a place value diagnostic assessment and teaching programme resource
References
Sharma, M. (2019). Dyscalculia and other mathematic difficulties.



