The main purpose of a working wall is to support children in their current learning and enable independence. If the wall is built with the children at the point of teaching, time spent displaying things on the wall outside of teaching time is minimised and what is on there is genuinely relevant. The children have seen the context in which it was put up and therefore are more likely to understand its purpose and be able to use it.
Pause for a moment and consider how you use working walls, washing lines, or other display space used for maths to support pupils’ learning. Do the children use them?
If I’m honest, when working walls first became ‘a thing’, I was guilty of having so much on my ‘to do’ list that displaying things on the wall just didn’t get done as often as it should and what was on there would become more like wallpaper. When I started to explore how I could interact more with the environment while teaching to make it work for me, I began to realise its full potential.
Here are my 4 suggestions to keep it manageable and useful:
(Disclaimer: walls not my own. Thank you to the schools who have kindly given me permission to share.)
1. Include models from current learning
Modelled examples from the previous lesson or earlier in the lesson can be used as a point of reference to support children’s working memory so that they don’t have to hold everything in their heads at once. Flipcharts or sugar paper are great for this.
Making sure the wall is easy to navigate and not too cluttered is important – more is not always better. A clear example from recent modelling can be extremely helpful to children.

This class in Lower Key Stage 2 were working on the structure of formal written subtraction with 3-digit numbers. Manipulatives were being used by the children alongside the teacher modelling on the flipchart. This was then popped up on the working wall for children to refer to throughout the sequence of learning.
As you can see, the teacher has modelled how to record the regrouping pictorially and in words to support children to both visualise and articulate the strategy when working independently.

This teacher has used a bar modelling approach to support children to unpick and understand the structure of a word problem.
This was an example that the class had worked through together.
The initial discussion centered around whether or not they needed to find 5/8 of 30. Children drew their own models to consider this and then a model was selected and drawn by the teacher. The part whole relationship was discussed and annotated and key information was labelled on the model. This was then linked to the calculations required to reach a solution and then added to the developing working wall for children to refer back to when practising independently.


Here, in these examples from Early Years, numbers are being represented in a variety of meaningful ways, either at the children’s height or large enough for them to see. Wall space has been used for two-dimensional display and then shelf tops for three-dimensional things to interact with. When talking about what was on this wall, a child referenced the outside environment, stating that, “When we park our bikes, one of them has a label with six spots on. That one gets parked in the ‘six’ space”.
2. Include key vocabulary
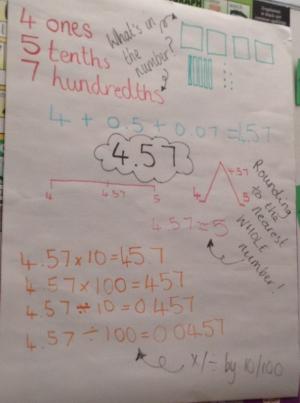 This class were beginning to explore how base-10 equipment could be used to support with understanding decimal place value and magnitude. The children were using the physical equipment and the teacher was recording the key language being used alongside a pictorial representation.
This class were beginning to explore how base-10 equipment could be used to support with understanding decimal place value and magnitude. The children were using the physical equipment and the teacher was recording the key language being used alongside a pictorial representation.

Here, with part of the array hidden, the children considered the question. Following a discussion, the teacher recorded their thinking and included language relating to equal parts and the whole.
A speaking frame to allow children to explain their resulting exploration was then left on the working wall for them to use should they wish.

This short speaking frame, on a Year 2 working wall, was taken from a pre-teaching session where children were securing understanding of 2-digit number place value.
They had been exploring 2-digit numbers using base-10 equipment and had found that 43 could be made up of:
4 tens and 3 ones
3 tens and 13 ones
2 tens and 23 ones
1 ten and 33 ones
0 tens and 43 ones
Bringing it back into the classroom and adding it to the working wall allowed the children who took part in the pre-teach to contribute to the strategy lesson. The teacher was able to connect the rehearsal from the intervention to the new learning in the classroom in a meaningful way.
A point to note about vocabulary…
Sometimes, trigger words on the working wall can be misleading. For example, left and take away are often shown as trigger words on a display for subtraction but consider how misleading that would be in the following problem:
Sam had 5 sweets left after Bob took 7. How many did Sam have to start with?
Because the problem contains the trigger words above, children could potentially interpret it as a subtraction problem. However, if children carefully consider the full context and structure of the problem, they will be able to identify that the two parts are actually known already (Sam’s 5 sweets and Bob’s 7) and it is the original whole that they need to find. They need to add the two known parts together.
3. Interact with the wall while teaching
We need to teach pupils how to use the contents of our working walls. If we sometimes teach from or at the wall, and point out useful information and prompts, demonstrating how we might use the wall ourselves by reviewing vocabulary and modelled examples, then pupils are more likely to use it as an aid.
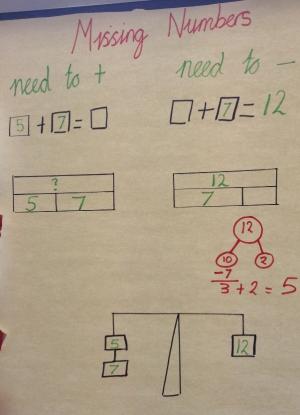 Focusing children’s attention on specific parts of the working wall when relevant, through a ‘what’s the same and what’s different?’ discussion, for example, will enable them to make connections and build on previous learning.
Focusing children’s attention on specific parts of the working wall when relevant, through a ‘what’s the same and what’s different?’ discussion, for example, will enable them to make connections and build on previous learning.
4. Promote deeper thinking
 During a sequence of learning about the relationships between perimeter and area, this working wall was used as a way for Year 6 children to develop and refine their thinking.
During a sequence of learning about the relationships between perimeter and area, this working wall was used as a way for Year 6 children to develop and refine their thinking.
Each child responded on a sticky note in their own way: some through written explanation; some through examples; some through diagrams and some through generalisations. The teacher was then able to pull out any misconceptions, e.g. around the relationship between a square and a rectangle, to discuss later as a group or class.

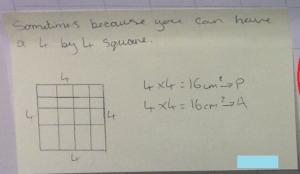

 Through interacting with the wall, some children developed their thinking further. They looked at examples from their peers, read the justifications and then added to their own thoughts, sometimes even changing their minds and proving their original ideas wrong with newly considered evidence.
Through interacting with the wall, some children developed their thinking further. They looked at examples from their peers, read the justifications and then added to their own thoughts, sometimes even changing their minds and proving their original ideas wrong with newly considered evidence.
 It’s often easier to spot errors that others have made, rather than our own. ‘Seek and destroy’ tasks are great for this as they are simple to write and can be based on errors the children have made, or are likely to make, themselves. The more children practise doing this and the more they consider how to generalise and come up with rules, the more naturally they will notice they’ve made an error ‘in the moment’ when problem solving.
It’s often easier to spot errors that others have made, rather than our own. ‘Seek and destroy’ tasks are great for this as they are simple to write and can be based on errors the children have made, or are likely to make, themselves. The more children practise doing this and the more they consider how to generalise and come up with rules, the more naturally they will notice they’ve made an error ‘in the moment’ when problem solving.
I am always interested in how teachers make their working walls work for them. Some have walls covered in clear, wipeable material so that whiteboard pens can be used to draw on them ‘live’ in lessons or fluency sessions. Others have beadstrings strung from side to side and giant tens frames and counters for children to manipulate. The creativeness of teachers and teaching assistants never ceases to amaze me.
To keep up to date: Join our Primary Subject Leaders’ mailing list



